W. Mora-FloresRevista Matemática, educación e Internet

Matemática 10^mo| Geometría | 2026.

Centro Educativo:

Walter Mora-Flores

| Autores

PDF

1. Geometría Analítica

Conocimientos			Habilidades específicas


Circunferencia			1. Representar gráficamente una circunferencia dado su centro y radio.

Centro			2. Representar algebraicamente una circunferencia.

Radio			3. Aplicar traslaciones a una circunferencia.

Recta secante			4. Resolver problemas de circunferencias.

Recta tangente			5. Clasificar puntos respecto a una circunferencia.

Recta exterior			6. Determinar si una recta es secante, tangente o exterior.

Rectas paralelas			7. Representar rectas secantes y tangentes.

Rectas perpendiculares			8. Analizar paralelismo y perpendicularidad.

			9. Aplicar la propiedad de tangencia.

			10. Usar software para representaciones.

1.1 Circunferencia

Situación problema.

Un movimiento sísmico es una vibración que se origina cuando una porción de la litosfera pierde estabilidad. El punto interior donde se libera la energía se llama hipocentro. Cuando las ondas sísmicas llegan a la superficie terres-tre y comienzan a propagarse sobre ella en todas direcciones, lo hacen a partir del epicentro, que es el punto superficial más cercano al hipocentro.

Las redes sismológicas modernas utilizan varias estaciones distribuidas en una región para registrar y analizar los sismos. En esta situación, se observa que tres estaciones cercanas de la red registran ondas de intensidad similar casi al mismo tiempo. Y en esta situación, más allá de estas estaciones la intensidad ya casi no es perceptible.

Zoom: Ejes (Use el ratón (o los dedos), sobre la figura)

Onda sísmica detectada por las estaciones A, B y C con intensidad similar.

Tomando como referencia la estación central (EC), la ubicación de las otras tres estaciones, expresadas en kilómetros, es la siguiente:

$∙$: Estación A: 24 kilómetros al norte y 15 kilómetros al este.
$∙$: Estación B: 30 kilómetros al norte y 6 kilómetros al este.
$∙$: Estación C: 15 kilómetros al sur y 10 kilómetros al este.

Si estas estaciones recibieron ondas de igual intensidad en un mismo intervalo de tiempo, entonces están aproxi-madamente a la misma distancia, medida sobre la superficie, del epicentro del sismo. Esto implica que dicho epicentro se localiza en un punto que está a igual distancia de A, B y C, es decir, en el centro de la circunferencia que pasa por los tres puntos.

Preguntas:

1.: ¿Cuál es la ubicación del epicentro con respecto a la estación central EC?
2.: ¿Cuál fue el radio de alcance de la onda sísmica?
3.: ¿Cómo se podría representar el comportamiento sísmico mediante una relación algebraica?

Definición 1 (Circunferencia).

Una circunferencia es el "lugar geométrico" de todos los puntos de un plano que están a una misma distancia fija, llamada radio, de un punto fijo llamado centro.

Circunferencia

Definición 2 (Círculo).

Un círculo es el conjunto de todos los puntos del plano cuya distancia a un punto fijo, llamado centro, es menor o igual a una longitud constante llamada radio.

El borde de un círculo es una curcunferencia.

Círculo

Ejemplo 1 (Trazado del "círculo central" en una cancha).

Para marcar el "círculo central" sobre el terreno de juego, es decir, la circunferencia que es borde de este círculo, se determina el punto central del campo y ponemos una estaca que servirá como centro. Luego tomamos una cuerda con la medida adecuada que servirá como radio (según las reglas del deporte), la tensamos y giramos para ir marcando la circunferencia, es decir, el borde del "círculo central".

Figura 1: Círculo central

Círculo central

1.2 Centro y radio

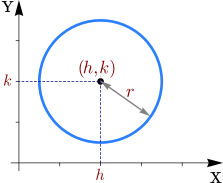
En un sistema de coordenadas cartesianas, diremos que el centro tiene coordenada $P (h, k)$ y el radio se denota con la letra $r$ , tal y como se muestra en la Figura 2

Figura 2: Centro

P (h, k)

y radio

r

Ejemplo 2.

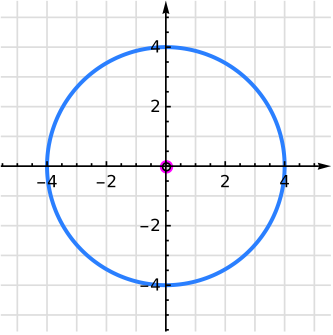
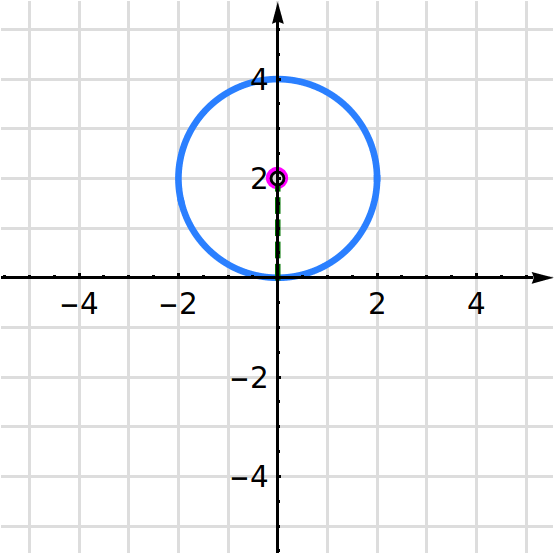
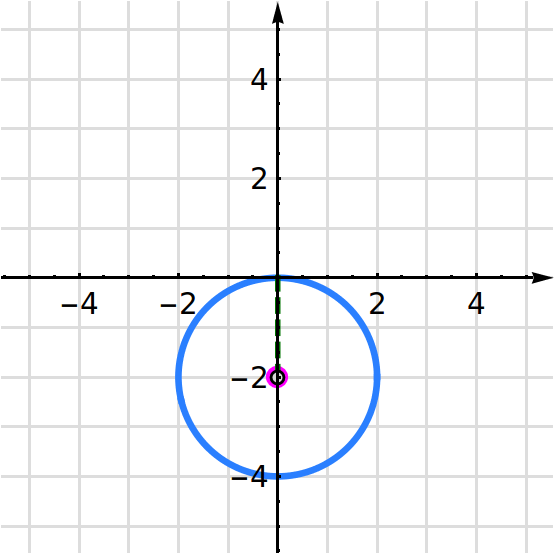
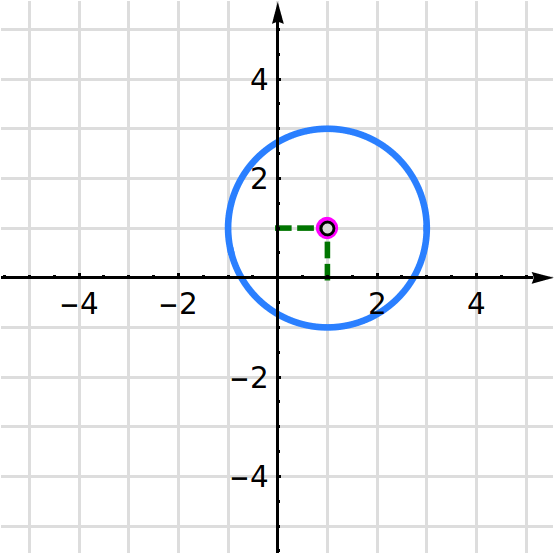
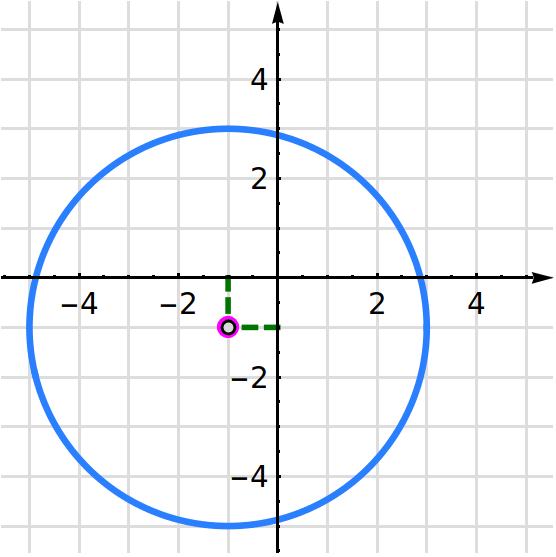
A continuación se muestran seis circunferencias. En cada ítem se indica el centro y el radio. En este caso el centro y el radio tienen coordenadas enteras. Vamos verificando que el centro y el radio que se enuncian, efectivamente coincida con la información de la representación gráfica.

1.

Circunferencia con centro en

(0, 0)

y radio

4

Figura 3:

2.

Circunferencia con centro en

(0, 2)

y radio

2

Figura 4:

3.

Circunferencia con centro en

(0, - 2)

y radio

2

Figura 5:

4.

Circunferencia con centro en

(1, 1)

y radio

2

Figura 6:

5.

Circunferencia con centro en

(- 1, - 1)

y radio

4

Figura 7:

6.

Circunferencia con centro en

(- 2, 2)

y radio

2

Figura 8:

Trabajo Cotidiano. En el siguiente script debes observar la circunferencia que se despliega y analizar para deducir cuál es el centro y cuál es el radio.

Las circunferencias en estos ejercicios tiene centro con coordenadas enteras y el radio también es un número entero. Escribimos la respuesta en los campos de texto y presionamos el botón "Verificar"

Para desplegar un nuevo ejercicio, presiona el botón "Siguiente ejercicio"

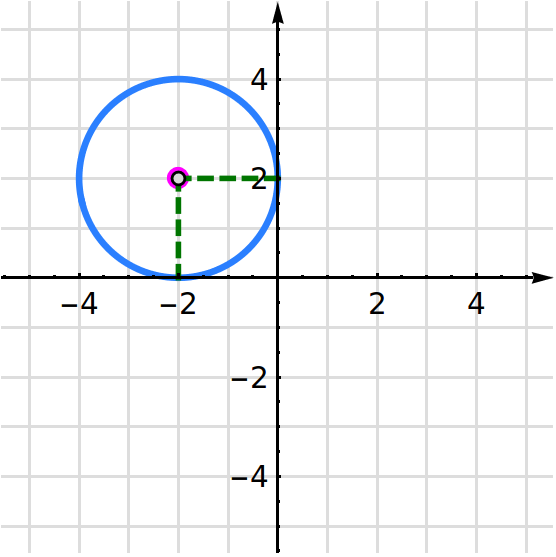
Ejercicio 1.1 Haz la representación gráfica de una circunferencia de centro

(1, 1)

y radio

r = 3

Ejercicio 1.2 Haz la representación gráfica de una circunferencia dado su centro

(- 2, 0)

y su radio

r = 2

1.3 Ecuación de la circunferencia

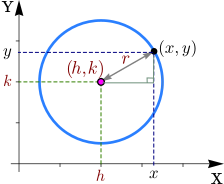
En un sistema de coordenadas cartesianas, podemos establecer una ecuación de una circunferencia de centro $P (h, k)$ y el radio $r$ , tal y como se muestra en la Figura 9

Para establecer esta ecuación podemos usar la fórmula de distancia (o lo que es lo mismo, el Teorema de Pitágoras) entre un punto $(x, y)$ en la circunferencia y el centro $(h, k)$ .

La distancia de $(x, y)$ a $(h, k)$ es $r$ , es decir,

\sqrt{{(x - h)}^{2} + {(y - k)}^{2}} = r

Y acostumbramos escribir esta ecuación de la circunferencia como

{(x - h)}^{2} + {(y - k)}^{2} = r^{2}

Figura 9: Centro

P (h, k)

y radio

r

Ejemplo 3.

En el siguiente script se despliega una circunferencia. Hay dos puntos, uno para el centro y otro para escalar (modificar) el radio. Cada vez que arrastramos cada punto, la ecuación de la circunferencia se actualiza. Se trata de observar y analizar como cambia el centro y el radio en la ecuación de la circunferencia.

Ejemplo 4.

A continuación, en cada ítem se indica el centro y el radio de una circunferencia. En este caso el centro y el radio tienen coordenadas enteras. Vamos a escribir la ecuación de la circunferencia

1.

Circunferencia con centro en

(0, 0)

y radio

4

Ecuación:

x^{2} + y^{2} = 16

Figura 10:

2.

Circunferencia con centro en

(0, 2)

y radio

2

Ecuación:

x^{2} + {(y - 2)}^{2} = 4

Figura 11:

3.

Circunferencia con centro en

(0, - 2)

y radio

2

Ecuación:

x^{2} + {(y + 2)}^{2} = 4

Figura 12:

4.

Circunferencia con centro en

(1, 1)

y radio

2

Ecuación:

{(x - 1)}^{2} + {(y - 1)}^{2} = 4

Figura 13:

5.

Circunferencia con centro en

(- 1, - 1)

y radio

4

Ecuación:

{(x + 1)}^{2} + {(y + 1)}^{2} = 16

Figura 14:

6.

Circunferencia con centro en

(- 2, 2)

y radio

2

Ecuación:

{(x + 2)}^{2} + {(y - 2)}^{2} = 4

Figura 15:

Trabajo Cotidiano.

Ejercicio 1.3 Dada una circunferencia de centro

(1, 1)

y radio

r = 3

, escribe su ecuación

{(x - 1)}^{2} + {(y - 1)}^{2} = 9

Ejercicio 1.4 Dada una circunferencia de centro

(- 1, 1)

y radio

r = 1

, escribe su ecuación

{(x + 1)}^{2} + {(y - 1)}^{2} = 1

Ejercicio 1.5 ¿Cuál es el radio de la circunferencia de ecuación

{(x - 2)}^{2} + {(y - 1)}^{2} = 2 ?

r^{2} = 2 ⟹ r = 2

Ejercicio 1.6 ¿Cuál es el radio y el centro de la circunferencia de ecuación

{(x - 2)}^{2} + {(y + 1)}^{2} = 9 ?

1.: Radio: $r^{2} = 9 ⟹ r = 3$
2.: Centro: Como la ecuación es ${(x - 2)}^{2} + {(y - - 1)}^{2} = 9$ entonces el centro es $(2, - 1)$

1.4 Puntos interior y exteriores a una circunferencia

Usando la misma fórmula para la distancia entre un punto arbitrario $Q (x, y)$ y el centro de una circunferencia de radio $r$ podemos establecer cuándo un punto está fuera de la circunferencia y cuándo está dentro de la circunferencia. Solo hay que notar si la distancia al centro es menor o mayor que el radio, como se muestra en la Figura 16

1.: El punto $Q (x, y)$ está en la circunferencia si
${(x - h)}^{2} + {(y - k)}^{2} = r^{2}$
2.: El punto $Q (x_{1}, y_{1})$ está afuera de la circunferencia si
${(x_{1} - h)}^{2} + {(y_{1} - k)}^{2} > r^{2}$
3.: El punto $Q (x_{2}, y_{2})$ en el interior de la circunferencia si
${(x_{2} - h)}^{2} + {(y_{2} - k)}^{2} < r^{2}$

Figura 16:

Ejemplo 5.

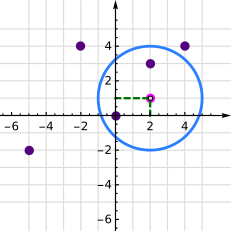
Considere la circunferencia de ecuación

{(x - 2)}^{2} + {(y - 1)}^{2} = 9

como se muestra en la Figura 17. ¿Cuáles de los siguientes puntos están en la circunferencia, fuera de la circunferencia o en el interior de la circunferencia?

1.: $(4, 4)$
2.: $(- 5, - 2)$
3.: $(2, 3)$
4.: $(0, 0)$
5.: $(- 2, 4)$

Figura 17:

Solución: Lo que debemos hacer es sustituir cada punto en la ecuación de la circunferencia

1.

Punto

(4, 4)

{(4 - 2)}^{2} + {(4 - 1)}^{2} = {(2)}^{2} + {(3)}^{2} = 4 + 9 = 13

Como $13 > 9$ , el punto es exterior a la circunferencia.

2.

Punto

(- 5, - 2)

{(- 5 - 2)}^{2} + {(- 2 - 1)}^{2} = {(- 7)}^{2} + {(- 3)}^{2} = 49 + 9 = 58

Como $58 > 9$ , el punto es exterior a la circunferencia.

3.

Punto

(2, 3)

{(2 - 2)}^{2} + {(3 - 1)}^{2} = {(0)}^{2} + {(2)}^{2} = 0 + 4 = 4

Como $4 < 9$ , el punto es interior a la circunferencia.

4.

Punto

(0, 0)

{(0 - 2)}^{2} + {(0 - 1)}^{2} = {(- 2)}^{2} + {(- 1)}^{2} = 4 + 1 = 5

Como $5 < 9$ , el punto es interior a la circunferencia.

5.

Punto

(- 2, 4)

{(- 2 - 2)}^{2} + {(4 - 1)}^{2} = {(- 4)}^{2} + {(3)}^{2} = 16 + 9 = 25

Como $25 > 9$ , el punto es exterior a la circunferencia.

Trabajo Cotidiano.

Ejercicio 1.7 Para la circunferencia dada por la ecuación

{(x + 2)}^{2} + y^{2} = 4

, determina si cada uno de los siguientes puntos está en la circunferencia, en su interior o en su exterior:

1.: $(- 2, 0)$
2.: $(0, 0)$
3.: $(- 4, 0)$
4.: $(- 2, 2)$
5.: $(- 2, \sqrt{3})$
6.: $(1, 0)$
7.: $(- 2, \sqrt{5})$
8.: $(- 5, 0)$

1.

Punto

(- 2, 0)

{(- 2 + 2)}^{2} + {(0)}^{2} = {(0)}^{2} + 0 = 0 + 0 = 0

Como $0 < 4$ , el punto es interior a la circunferencia.

2.

Punto

(0, 0)

{(0 + 2)}^{2} + {(0)}^{2} = {(2)}^{2} + 0 = 4 + 0 = 4

Como $4 = 4$ , el punto está en la circunferencia.

3.

Punto

(- 4, 0)

{(- 4 + 2)}^{2} + {(0)}^{2} = {(- 2)}^{2} + 0 = 4 + 0 = 4

Como $4 = 4$ , el punto está en la circunferencia.

4.

Punto

(- 2, 2)

{(- 2 + 2)}^{2} + {(2)}^{2} = {(0)}^{2} + 4 = 0 + 4 = 4

Como $4 = 4$ , el punto está en la circunferencia.

5.

Punto

(- 2, \sqrt{3})

{(- 2 + 2)}^{2} + {(\sqrt{3})}^{2} = 0 + 3 = 3

Como $3 < 4$ , el punto es interior a la circunferencia.

6.

Punto

(1, 0)

{(1 + 2)}^{2} + {(0)}^{2} = {(3)}^{2} + 0 = 9 + 0 = 9

Como $9 > 4$ , el punto es exterior a la circunferencia.

7.

Punto

(- 2, \sqrt{5})

{(- 2 + 2)}^{2} + {(\sqrt{5})}^{2} = 0 + 5 = 5

Como $5 > 4$ , el punto es exterior a la circunferencia.

8.

Punto

(- 5, 0)

{(- 5 + 2)}^{2} + {(0)}^{2} = {(- 3)}^{2} + 0 = 9 + 0 = 9

Como $9 > 4$ , el punto es exterior a la circunferencia.

2. Polígonos

Conocimientos			Habilidades específicas


Polígonos			11. Determinar perímetros y áreas de polígonos.

Lado			12. Determinar ángulos internos y externos.

Radio			13. Determinar apotema y radio.

Apotema			14. Calcular áreas con coordenadas.

Ángulo central			15. Resolver problemas con polígonos.

Ángulo interno			16. Estimar áreas irregulares.

Ángulo externo			17. Usar software de geometría.

Diagonal

Perímetro

Área

Relaciones métricas

3. Visualización Espacial

Conocimientos			Habilidades específicas


Visualización espacial			18. Identificar radio y diámetro de una esfera.

Esfera			19. Identificar elementos de un cilindro circular recto.

Cilindro circular recto			20. Determinar figuras de secciones planas.

Base			21. Reconocer elipses en contextos reales.

Superficie lateral

Radio

Diámetro

Sección plana

Elipse

Traducción LaTeX a HTML con Make4ht y JavaScritpt. W. Mora (2225). "Generar webs interactivas con LaTeX"

Traducción LaTeX a HTML con Make4ht y JavaScritpt. W. Mora (Agosto-2025). "Generar una Web Interactica con LaTeX (usando Make4ht e IA)"

1. Geometría Analítica

1.1 Circunferencia

1.2 Centro y radio

Determine el centro y el radio de la circunferencia

1.3 Ecuación de la circunferencia

Una ecuación de la circunferencia

1.4 Puntos interior y exteriores a una circunferencia

2. Polígonos

3. Visualización Espacial